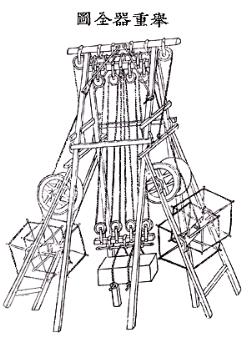
고정·움직도르래 원리 이용해 18C 제작
 |
수원 화성은 서쪽으로 팔달산을 끼고 동쪽의 낮은 언덕과 평지를 따라 쌓은 성으로, 우리나라 성곽(城郭) 가운데 가장 완벽한 구조를 갖추고 있다.
이 성(城)은 1794∼1796(정조 18∼20)년까지 2년 6개월 동안 쌓았는데, 이와 관련된 모든 일, 제도(制度), 의식(儀式) 등을 자세히 기록한공사 보고서인'화성성역의궤(華城城役儀軌)'가 간행되어 수원 화성의 모든 것을 알 수 있다.
성쌓기 방법은 예로부터 이어져 오던 우리 고유의 기술과 경험을 바탕으로 실학자 유형원(柳馨遠)과 정약용(丁若鏞) 등의 새로운 과학지식을 활용하여 무거운 돌을 들어 올리는 기구인 녹로와 거중기(擧重機)를 만들어 사용하였을 뿐만 아니라, 건축 재료를 규격화하는 등 당시의 첨단 과학기술을 모두 반영하고 있다.
수원 화성은 가로 1.5m, 세로 1m, 무게 2000㎏ 정도의 돌을 5m 높이로 쌓아서 만든 성으로 이 성을 쌓는데 소요된 기간은 원래 10년을 걸리는 것으로 계산 되었지만 불과 2년 반이라는 단기간 내에 완성하였다. 이것은 정약용이 고정도르래와 움직도르래의 원리를 이용하여 고안한 첨단건축 장비인 '거중기'가 있었기 때문에 가능하였다.
현재의 기중기와 같은 용도인 거중기는 위쪽의 고정도르래 4개와 그 아래의 움직도르래 4개에 들어올리려는 물체가 매달리게 되어있고, 이것이 위쪽 좌우 2개의 큰 고정도르래에 연결된 후 다시 녹로인 고정도르래에 감아 돌려져서 물체를 들어올릴 수 있는 구조로 되어 있다.
따라서 그 수(n)에 따라 물체 무게의 1/2n에 해당하는 힘으로 물체를 움직일 수 있는 움직도르래의 원리에 의해, 움직도르래의 수가 4개인 거중기는 이론상 1/24=1/16의 힘으로 물체를 들어올릴 수 있는 것이다. 이것은 달리 말하면 한 사람이 16배의 힘을 낼 수 있다는 것과 같은 것이다.
하지만 선학인 정약용선생은 '정다산전서(丁茶山全書)'-(기중도설)起重圖說'에서 상하 4개씩의 도르래를 사용하면 전체로 25배의 힘을 낸다고 적고 있다. 또한'화성성역의궤'의 기록에는 화성을 쌓을 때 좌우 각각 15명의 남자들이 1만 2000근(7200㎏)의 돌을 들어 올릴 수 있어서 한 사람이 400근(240㎏)의 무게를 들어 올릴 수 있었다고 하여 실제 사용에는 약간의 차이가 남는다. 이렇게 정약용과 현대의 계산법이 차이가 나는 이유는 무엇일까?
움직도르래의 경우 물체를 끄는 길이가 물체의 움직인 거리의 2배가 되어 실제 물건을 들어 올리게 위해 사용되는 힘은 1/2n=1/8로 반감된다. 즉, 현대의 물리학이론에서 볼 때 움직도르래가 4개인 거중기를 통해 물건을 들어 올릴 때는 실제로 한 사람이 16배가 아닌 8배의 힘을 낼 수 있다.
하지만 정약용의 계산 착오인지는 몰라도 25배로 주장하고 있는 것은 착각일까? 아니면 우리가 거중기의 구조 즉, 지렛대의 역할을 하는 축바퀴의 힘을 간과하고 있는 것은 아닌지? 되돌아보고 싶다. 만약 축바퀴의 중심부터 바퀴살 끝까지의 거리(r)와 축의 반지름(r)을 비교하여 6.25가 나온다면, 움직도르래 2개에서 얻는 힘 4배를 곱하면 25배가 되기 때문이다. 선학의 착각일까 우리의 착오일까?
 |
| ▲ 윤용현 국립중앙과학관 학예연구관 |